Chapter : Motion in one Dimension
Motion With Uniform Acceleration
Let  = Initial velocity (at t = 0),
= Initial velocity (at t = 0),  = Velocity of the particle after time t,
= Velocity of the particle after time t,  = Acceleration (uniform),
= Acceleration (uniform),  = Displacement of the particle during time 't'
= Displacement of the particle during time 't'
(a) Acceleration,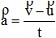 [Because of uniform acceleration, this acceleration is instantaneous as well average acceleration]. From above equation
[Because of uniform acceleration, this acceleration is instantaneous as well average acceleration]. From above equation  =
=  +
+  t ....(i)
t ....(i)
(b) Displacement = Average velocity × time, ....(ii)
....(ii)
[This is very useful equation, when acceleration is not given]
(c) From (i) and (ii) =
=  t + (1/2)
t + (1/2)  t2 ....(iii)
t2 ....(iii)
Again from (i) and (iii)
 =
=  t − (1/2)
t − (1/2)  t2.
t2.
[Here negative sign does not indicate that retardation is occurring]
(d) From (i) and (ii) 2 =
2 =  2 + 2
2 + 2 
 .....(iv)
.....(iv)
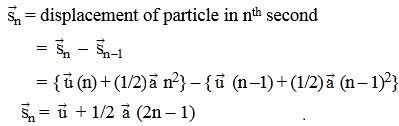
[This equation is dimensionally non balanced because we have substituted value of t = 1s and second is neglected that's why it seems to be unbalanced]
Equations (i), (iii) and (iv) one called 'equations of motion' and are very useful in solving the problems of motion along a straight line with constant acceleration.
Note :
(i) These equations can be applied only and only when acceleration is constant. In case of circular motion or simple harmonic motion as acceleration is not constant (due to change in direction or magnitude) so these equation can not be applied.
(ii) =
=  +
+  t and
t and  =
=  t + (1/2)
t + (1/2) t2 are vector equation, while
t2 are vector equation, while

 =
= 
 + 2
+ 2

⇒ v2 = u2 + 2
 is a scalar equation
is a scalar equation
(iii) If the velocity and acceleration are collinear, we conventionally take the direction of motion to be positive, so equation of motions becomes v = u + at, s = ut + (1/2) at2, v2= u2+ 2as
If the velocity and acceleration are anti-parallel then, v = u – at, s = ut – (1/2) at2 and v2 = u2 – 2as
 = Initial velocity (at t = 0),
= Initial velocity (at t = 0),  = Velocity of the particle after time t,
= Velocity of the particle after time t,  = Acceleration (uniform),
= Acceleration (uniform),  = Displacement of the particle during time 't'
= Displacement of the particle during time 't'(a) Acceleration,
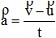 [Because of uniform acceleration, this acceleration is instantaneous as well average acceleration]. From above equation
[Because of uniform acceleration, this acceleration is instantaneous as well average acceleration]. From above equation  =
=  +
+  t ....(i)
t ....(i)(b) Displacement = Average velocity × time,
 ....(ii)
....(ii)[This is very useful equation, when acceleration is not given]
(c) From (i) and (ii)
 =
=  t + (1/2)
t + (1/2)  t2 ....(iii)
t2 ....(iii)Again from (i) and (iii)
 =
=  t − (1/2)
t − (1/2)  t2.
t2. [Here negative sign does not indicate that retardation is occurring]
(d) From (i) and (ii)
 2 =
2 =  2 + 2
2 + 2 
 .....(iv)
.....(iv)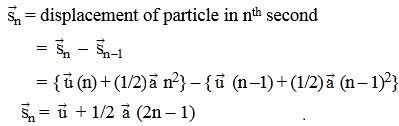
[This equation is dimensionally non balanced because we have substituted value of t = 1s and second is neglected that's why it seems to be unbalanced]
Equations (i), (iii) and (iv) one called 'equations of motion' and are very useful in solving the problems of motion along a straight line with constant acceleration.
Note :
(i) These equations can be applied only and only when acceleration is constant. In case of circular motion or simple harmonic motion as acceleration is not constant (due to change in direction or magnitude) so these equation can not be applied.
(ii)
 =
=  +
+  t and
t and  =
=  t + (1/2)
t + (1/2) t2 are vector equation, while
t2 are vector equation, while 
 =
= 
 + 2
+ 2

⇒ v2 = u2 + 2

 is a scalar equation
is a scalar equation(iii) If the velocity and acceleration are collinear, we conventionally take the direction of motion to be positive, so equation of motions becomes v = u + at, s = ut + (1/2) at2, v2= u2+ 2as
If the velocity and acceleration are anti-parallel then, v = u – at, s = ut – (1/2) at2 and v2 = u2 – 2as
Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions