Chapter : Motion in one Dimension
Motion Under Gravity
Ideal Motion :
The most important example of motion in a straight line with constant acceleration is motion under gravity. In case of motion under gravity unless stated it is taken for granted that.
(i) The acceleration is constant, i.e. =
= 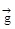 = 9.8 m/s2 and directed vertically downwards.
= 9.8 m/s2 and directed vertically downwards.
(ii) The motion is in vacuum i.e. viscous force or thrust of the medium has no effect on the motion.
Now in the light of above assumptions, there are two possibilities.
10.1 Body Falling Freely Under Gravity :
Taking initial position as origin and direction of motion (i.e. downward direction) as positive, here we have u = 0 (as body starts from rest)
a = + g
(as acceleration is in the direction of motion)
So, if the body acquires velocity v after falling a distance h in time t, equations of motion viz v = u + at , s = ut + at2 and v2 = u2 + 2as reduces to
at2 and v2 = u2 + 2as reduces to
v = gt ....(1)
h = gt2 ....(2)
gt2 ....(2)
v2 = 2gh ....(3)
These equations can be used to solve most of the problems of freely falling as
Note :
(a) If the body is dropped from a height H, as in time t, it has fallen a distance h from its initial position, the height of the body from the ground will be h' = H – h, with h = 1/2 gt2.
(b) As h = (1/2) gt2 i.e. h ∝ t2, distance fallen in time t, 2t, 3t etc. will be in the ratio of 12: 22: 32: ––––––– i.e. square of integers.
(c) The distance fallen in nth sec.,
hn – hn –1 = (1/2) g(n)2 – (1/2) g(n – 1)2= (1/2) g(2n –1)
So distance fallen in Ist, IInd, IIIrd sec will be in the ratio 1 : 3 : 5 i.e. odd integers only.
10.2 Body is projected vertically up :
Taking initial position as origin and direction of motion (i.e. vertically up) as positive, here we have v = 0 [as at the highest point, velocity = 0], a = – g [as acceleration is downwards while motion upwards].
So, if the body is projected with velocity u and reaches the highest point at a distance h above the ground in time t, the equations of motion viz v = u + at, s = ut + at2and v2= u2+ 2as reduces to
at2and v2= u2+ 2as reduces to
0 = u – gt
h = ut – 1/2 gt2
and 0 = u2– 2gh
or u = gt ....(1)
h = 1/2 gt2 ...(2)
(∴ u = gt), u2 = 2 gh ....(3)
These equations can be used to solve most of the problems of bodies projected vertically up as, if
Discussion :
From cases (10.1) and (10.2) it is clear that :
(a) In case of motion under gravity for a given body, mass, acceleration and mechanical energy remains constant while speed, velocity, momentum, kinetic energy and potential energy changes.
(b) The motion is independent to the mass of the body as in any equation of motion mass is not involved. This is why a heavy and light body when released from same height reaches the ground simultaneously and with same velocity.
i.e. t =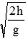
and v =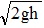
However, momentum, kinetic energy or potential energy depends on the mass of the body (all ∝ mass)
(c) As from case (b) time taken to reach a height h,
tU =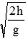
And from case (a) time taken to fall down through a distance h,
tD =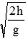
so tU= tD=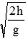
So in case of motion under gravity time taken to go up is equal to the time taken to fall down through the same distance.
(d) If a body projected vertically up reaches a height h then from case (b), u =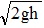 and if a body falls freely through a height h from case (a),
and if a body falls freely through a height h from case (a),
v =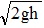
So in case of motion under gravity the speed with which a body is projected up is equal to the speed with which it comes back to the point of projection
The most important example of motion in a straight line with constant acceleration is motion under gravity. In case of motion under gravity unless stated it is taken for granted that.
(i) The acceleration is constant, i.e.
 =
= 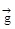 = 9.8 m/s2 and directed vertically downwards.
= 9.8 m/s2 and directed vertically downwards.(ii) The motion is in vacuum i.e. viscous force or thrust of the medium has no effect on the motion.
Now in the light of above assumptions, there are two possibilities.
10.1 Body Falling Freely Under Gravity :
Taking initial position as origin and direction of motion (i.e. downward direction) as positive, here we have u = 0 (as body starts from rest)
a = + g
(as acceleration is in the direction of motion)
So, if the body acquires velocity v after falling a distance h in time t, equations of motion viz v = u + at , s = ut +
 at2 and v2 = u2 + 2as reduces to
at2 and v2 = u2 + 2as reduces to v = gt ....(1)
h =
 gt2 ....(2)
gt2 ....(2)v2 = 2gh ....(3)
These equations can be used to solve most of the problems of freely falling as
| If t is given | If h is given | If v is given |
|---|---|---|
| From eq. (1) & (2) | From eq. (2) & (3) | From eq. (3) & (1) |
| v = gt | t= 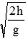 | t=  |
h =  gt2 gt2 | v= 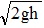 |  |
 |  |  |
Note :
(a) If the body is dropped from a height H, as in time t, it has fallen a distance h from its initial position, the height of the body from the ground will be h' = H – h, with h = 1/2 gt2.
(b) As h = (1/2) gt2 i.e. h ∝ t2, distance fallen in time t, 2t, 3t etc. will be in the ratio of 12: 22: 32: ––––––– i.e. square of integers.
(c) The distance fallen in nth sec.,
hn – hn –1 = (1/2) g(n)2 – (1/2) g(n – 1)2= (1/2) g(2n –1)
So distance fallen in Ist, IInd, IIIrd sec will be in the ratio 1 : 3 : 5 i.e. odd integers only.
10.2 Body is projected vertically up :
Taking initial position as origin and direction of motion (i.e. vertically up) as positive, here we have v = 0 [as at the highest point, velocity = 0], a = – g [as acceleration is downwards while motion upwards].
So, if the body is projected with velocity u and reaches the highest point at a distance h above the ground in time t, the equations of motion viz v = u + at, s = ut +
 at2and v2= u2+ 2as reduces to
at2and v2= u2+ 2as reduces to 0 = u – gt
h = ut – 1/2 gt2
and 0 = u2– 2gh
or u = gt ....(1)
h = 1/2 gt2 ...(2)
(∴ u = gt), u2 = 2 gh ....(3)
These equations can be used to solve most of the problems of bodies projected vertically up as, if
| If t is given | If h is given | If v is given |
|---|---|---|
| From eq. (1) & (2) | From eq. (2) & (3) | From eq. (3) & (1) |
| u = gt | t= 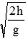 | t= u/g |
h =  gt2 gt2 | u = 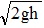 | h = u2/2g |
 |  |  |
Discussion :
From cases (10.1) and (10.2) it is clear that :
(a) In case of motion under gravity for a given body, mass, acceleration and mechanical energy remains constant while speed, velocity, momentum, kinetic energy and potential energy changes.
(b) The motion is independent to the mass of the body as in any equation of motion mass is not involved. This is why a heavy and light body when released from same height reaches the ground simultaneously and with same velocity.
i.e. t =
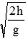
and v =
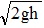
However, momentum, kinetic energy or potential energy depends on the mass of the body (all ∝ mass)
(c) As from case (b) time taken to reach a height h,
tU =
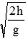
And from case (a) time taken to fall down through a distance h,
tD =
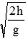
so tU= tD=
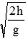
So in case of motion under gravity time taken to go up is equal to the time taken to fall down through the same distance.
(d) If a body projected vertically up reaches a height h then from case (b), u =
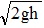 and if a body falls freely through a height h from case (a),
and if a body falls freely through a height h from case (a), v =
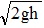
So in case of motion under gravity the speed with which a body is projected up is equal to the speed with which it comes back to the point of projection
Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions