Chapter : Gravitation
satellite
a) Celestial bodies revolving round the gravitational field of the planets is called satellite.
b) Satellites are of two types -
• Natural satellites - As moon is a satellite of the earth.
• Artificial satellites - They are launched by man such as Rohini, Aryabhatt etc.
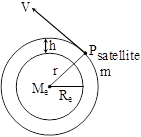
c) Let a satellite of mass 'm' revolves in a circular orbit with radius 'r' around the earth. The necessary centripetal force needed for circular motion is provided by the gravitational force of the earth.
so,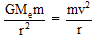
Where Me = mass of earth
v = Orbital velocity of satellite
r = Radius of satellite's orbit = Re + h = orbital radius
Re= Radius of earth
h = The height of the satellite above the earth's surface
g = Acceleration due to gravity on the surface of the earth.
d) Orbital velocity of satellite :
i) v =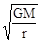 =
=  =
= 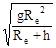
ii) From this expression,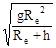 , it is clear that orbital velocity does not depend on the mass of satellite butit depends on the height of the satellite above the earth's surface (h). Greater the height of satellite, smalleris the orbital velocity.
, it is clear that orbital velocity does not depend on the mass of satellite butit depends on the height of the satellite above the earth's surface (h). Greater the height of satellite, smalleris the orbital velocity.
Note :- This proves that keplers II Law is true.
iii) If a satellite is very close to the earths surface (h << Re), then h will be negligible as compared to R than the orbital speed of satellite is given by
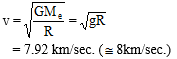
e) Period of Revolution :
(i) The time taken by the satellite for completing one revolution of earth is called as period of revolution of satellite.
(ii) Period of Revolution of a satellite is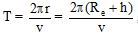 where 'T' is the time period of a satellite at a height 'h'.
where 'T' is the time period of a satellite at a height 'h'.
(iii)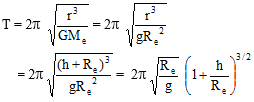
(iv) It is evident from the above expression that T2 ∝ r3 i.e kepler's III law is true for circular motion also.
(v) For a satellite revolving very close to the surface of earth (h << Re),
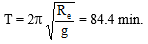
therefore, the minimum time period of the satellite revolving very close to the surface of earth is 84.4 min.
(vi)From the expression '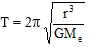 we can say that time period of satellite depends on its orbital radius T2 ∝ r3
we can say that time period of satellite depends on its orbital radius T2 ∝ r3
As the radius increases, simultaneously time period also increase.
f) Energy of Satellite : When satellite is revolving in the orbit of radius 'r' then
(i)Potential energy of satellite :
Potential energy =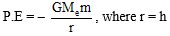
(ii) Kinetic energy of satellite :
Kinetic energy = K. E. =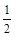 mv2 =
mv2 = 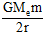
(iii) Total energy of satellite
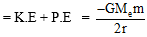
(iv) We can say that :Total energy of satellite =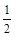 (Potential energy of satellite) = - Kinetic Energy of satellite.
(Potential energy of satellite) = - Kinetic Energy of satellite.
g) Binding Energy of satellite :
(i) Binding energy is the energy given to satellite in order that the satellite escape away form its orbit.
Binding Energy = - Total Energy =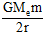 (i.e equal to kinetic energy)
(i.e equal to kinetic energy)
If energy equals to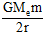 , is provided to the satellite, it will escape away from the gravitational field of the planet.
, is provided to the satellite, it will escape away from the gravitational field of the planet.
(ii) Unless a revolving satellite gets extra energy, it would not leave its orbit. If the kinetic energy of a satellite happens to increase to two times, the satellite would escape.
(iii) If the orbital velocity of a satellite revolving close to the earth happens to increase to √2 times, the satellite would escape. That means if orbital velocity increases to 41.4% , satellite would leave the orbit.
(iv) Total energy of satellite is always negative. When the energy of the satellite is negative, it moves in either a circular or an elliptical orbit.
(v) Binding Energy = Kinetic Energy = - (Total Energy) = -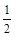 (Potential Energy)
(Potential Energy)
b) Satellites are of two types -
• Natural satellites - As moon is a satellite of the earth.
• Artificial satellites - They are launched by man such as Rohini, Aryabhatt etc.
c) Let a satellite of mass 'm' revolves in a circular orbit with radius 'r' around the earth. The necessary centripetal force needed for circular motion is provided by the gravitational force of the earth.

so,
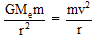
Where Me = mass of earth
v = Orbital velocity of satellite
r = Radius of satellite's orbit = Re + h = orbital radius
Re= Radius of earth
h = The height of the satellite above the earth's surface
g = Acceleration due to gravity on the surface of the earth.
d) Orbital velocity of satellite :
i) v =
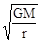 =
=  =
= 
ii) From this expression,
 , it is clear that orbital velocity does not depend on the mass of satellite butit depends on the height of the satellite above the earth's surface (h). Greater the height of satellite, smalleris the orbital velocity.
, it is clear that orbital velocity does not depend on the mass of satellite butit depends on the height of the satellite above the earth's surface (h). Greater the height of satellite, smalleris the orbital velocity. Note :- This proves that keplers II Law is true.
iii) If a satellite is very close to the earths surface (h << Re), then h will be negligible as compared to R than the orbital speed of satellite is given by
e) Period of Revolution :
(i) The time taken by the satellite for completing one revolution of earth is called as period of revolution of satellite.
(ii) Period of Revolution of a satellite is
 where 'T' is the time period of a satellite at a height 'h'.
where 'T' is the time period of a satellite at a height 'h'.(iii)
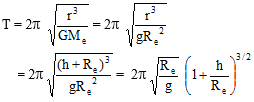
(iv) It is evident from the above expression that T2 ∝ r3 i.e kepler's III law is true for circular motion also.
(v) For a satellite revolving very close to the surface of earth (h << Re),
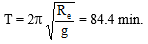
therefore, the minimum time period of the satellite revolving very close to the surface of earth is 84.4 min.
(vi)From the expression '
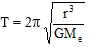 we can say that time period of satellite depends on its orbital radius T2 ∝ r3
we can say that time period of satellite depends on its orbital radius T2 ∝ r3 As the radius increases, simultaneously time period also increase.
f) Energy of Satellite : When satellite is revolving in the orbit of radius 'r' then
(i)Potential energy of satellite :
Potential energy =
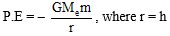
(ii) Kinetic energy of satellite :
Kinetic energy = K. E. =
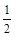 mv2 =
mv2 = 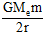
(iii) Total energy of satellite
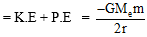
(iv) We can say that :Total energy of satellite =
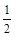 (Potential energy of satellite) = - Kinetic Energy of satellite.
(Potential energy of satellite) = - Kinetic Energy of satellite.g) Binding Energy of satellite :
(i) Binding energy is the energy given to satellite in order that the satellite escape away form its orbit.
Binding Energy = - Total Energy =
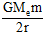 (i.e equal to kinetic energy)
(i.e equal to kinetic energy)If energy equals to
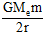 , is provided to the satellite, it will escape away from the gravitational field of the planet.
, is provided to the satellite, it will escape away from the gravitational field of the planet.(ii) Unless a revolving satellite gets extra energy, it would not leave its orbit. If the kinetic energy of a satellite happens to increase to two times, the satellite would escape.
(iii) If the orbital velocity of a satellite revolving close to the earth happens to increase to √2 times, the satellite would escape. That means if orbital velocity increases to 41.4% , satellite would leave the orbit.
(iv) Total energy of satellite is always negative. When the energy of the satellite is negative, it moves in either a circular or an elliptical orbit.
(v) Binding Energy = Kinetic Energy = - (Total Energy) = -
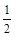 (Potential Energy)
(Potential Energy) Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions