Mathematics

Example :  Find the L.C.M. and H.C.F. of the following pairs of integers by applying the Fundamental theorem of Arithmetic Method (Using the Prime Factorisation Method).
(i) 26 and 91
(ii) 1296 and 2520
(iii) 17 and 25

Solution:

(i) Since, 26 = 2 × 13 and, 91 = 7 × 13

∴ L.C.M. = Product of each prime factor with highest powers = 2 × 13 × 7 = 182. (Answer)
i.e., L.C.M. (26, 91) = 182. (Answer)
H.C.F. = Product of common prime factors with lowest powers. = 13.
i.e., H.C.F (26, 91) = 13.

(ii) Since, 1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 = 2⁴ × 3⁴ and, 2520 = 2 × 2 × 2 × 3 × 3 × 5 × 7 = 2³ × 3² × 5 × 7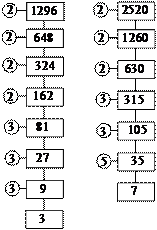

∴L.C.M. = Product of each prime factor with highest powers = 2⁴ × 3⁴ × 5 × 7 = 45,360
i.e., L.C.M. (1296, 2520) = 45,360 (Answer)
H.C.F. = Product of common prime factors with lowest powers. = 2³ × 3² = 8 × 9 = 72
i.e., H.C.F. (1296, 2520) = 72. (Answer)

(iii) Since, 17 = 17 and, 25 = 5 × 5 = 5²
∴ L.C.M. = 17 × 5² = 17 × 25 = 425 and, H.C.F. = Product of common prime factors with lowest powers = 1, as given numbers do not have any common prime factor.

In example 19 (i) : Product of given two numbers = 26 × 91 = 2366 and, product of their L.C.M. and H.C.F. = 182 × 13 = 2366
∴ Product of L.C.M and H.C.F of two given numbers = Product of the given numbers

In example 19 (ii) : Product of given two numbers = 1296 × 2520 = 3265920 and, product of their L.C.M. and H.C.F. = 45360 × 72 = 3265920
∴L.C.M. (1296, 2520) × H.C.F. (1296, 2520) = 1296 × 2520

In example 19 (iii) :
The given numbers 17 and 25 do not have any common prime factor. Such numbers are called co-prime numbers and their H.C.F. is always equal to 1 (one), whereas their L.C.M. is equal to the product of the numbers. But in case of two co-prime numbers also, the product of the numbers is always equal to the product of their L.C.M. and their H.C.F.
As, in case of co-prime numbers 17 and 25;
H.C.F. = 1; L.C.M. = 17 × 25 = 425;
Product of numbers = 17 × 25 = 425 and product of their H.C.F. and L.C.M. = 1 × 425 = 425.